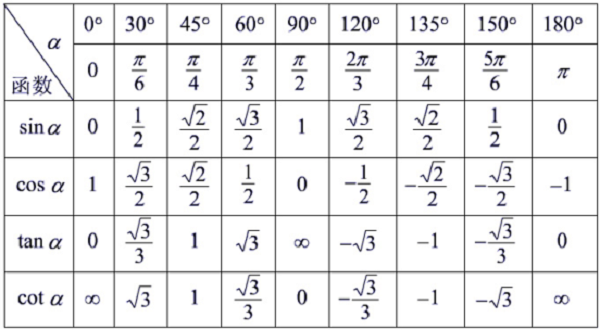
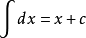三角函数诱导公式涉及到的公式相当多,但记忆诱导公式有一个统一的口诀:奇变偶不变,符号看象限。多少年来,参考书这么写,老师们这么教,但是教材却从没有简化,原因何在?
三角函数诱导公式口诀解析
任意一个角都可以表示为的形式。当把任意角化为该形式后,利用口诀“奇变偶不变,符号看象限”,就能把任意角转化到之间,即初中所学,学生熟悉的锐角三角函数值问题了。
下面对该口诀进行必要的解析:
1.“奇”与“偶”:是指把任意角化为kπ/2+α(-π/2<α<π/2,k∈z)的形式中的奇偶性,即是奇数还是偶数;
2.“变”与“不变”:是指三角函数的名称改变与否,即若变,则正弦变余弦、余弦变正弦、正切变余切、余切变正切。
综合以上,“奇变偶不变”是说,把任意角化为kπ/2+α的形式后,若奇数则三角函数名称改变,若是偶数则三角函数名称不改变。
3.“象限”:是指把任意角化为kπ/2+α的形式后,假设α∈{0,π/2}时,kπ/2+α所在的象限。
4.“符号”:是指在确定kπ/2+α所在的象限后,相应的原三角函数值的符号(如下图)。
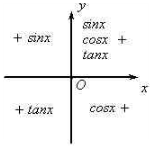
诱导公式记忆口诀:
“奇变偶不变,符号看象限”。“奇、偶”指的是π/2的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。(反之亦然成立)“符号看象限”的含义是:把角α看做锐角,不考虑α角所在象限,看n·(π/2)±α是第几象限角,从而得到等式右边是正号还是负号。符号判断口诀:“一全正;二正弦;三正切;四余弦”。这十二字口诀的意思就是说:第一象限内任何一个角的四种三角函数值都是“+”;第二象限内只有正弦是“+”,其余全部是“-”;第三象限内只有正切和余切是“+”,其余全部是“-”;第四象限内只有余弦是“+”,其余全部是“-”。
诱导公式的内在联系
教材中所给的诱导公式,集中体现了数学中的化归与转化思想。在求任意角的三角函数值时,其基本思路为:负角→正角→(0,π)内的角→(0,π/2)内的角。
根据这个思路,运用口诀“奇变偶不变,符号看象限”化简,就不可能充分地体现出来,并且在口诀中,任意角所在象限的判断也是相当麻烦的。
下面,针对教材中所给的三角函数诱导公式及化归与转化思路,将它们划分为三类诱导公式。
① 不变,奇-偶+(繁角→简角)
如果任意角可以表示成kπ+α(-π<α<π,k∈z),即含有π的整数倍,则选用第一类诱导公式。利用该公式可将繁杂角化为简单的角。
第一类诱导公式:正弦函数、余弦函数的名称不改变,化简后的符号随k的奇偶性而改变──奇数-、偶数+。即